Dynamic Neural Architecture(DNA)
Check out my project on GitHub
This is my little research project. I try to make a dynamic neural network with one layer for decentralized artificial intelligence(DAI) purpose. We can dynamic delete and create neural cell node. This idea is inspired by Hebbian theory. I am not sure is will work or not. Let’s see!
Fire together wire together(Hebbian theory)
Let us assume that the persistence or repetition of a reverberatory activity (or “trace”) tends to induce lasting cellular changes that add to its stability. … When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.
– From Hebbian theory
So, In my understanding, for a AI model neural, let’s say the assumption of ‘the persistence or repetition of a reverberatory activity’ is the training process, the ‘cell’ is a neural structure int the model, ‘When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.’ means if neural A is activated, A will active(fire) neural B sequently.
How about to make a AI model base on this theory.
Before I design my model, I try to modify some rule in Hebbian theory. In Hebbian theory, cell A will be activated before B, then cell B will be activated by cell A. But, to make a parallel architecture for my future plan about my decentralized model. I am going to activate neural A and neral B. Because In my opinion, they will finally be activated for a same activity no matter the order.
Neural cell
So. In my idea, neural cell can be assumed as a weighted signal function minus a signal leaking[Hodgkin–Huxley model].
So, our neural cell can be simplified as ->
Yes, we can also replace thie simple function to a complicate function such as KAN model.
Can it work?
In common, the universal approximation theorem said a feed-forward network with a single hidden layer containing a finite number of neurons can approximate any continuous function. So, I think If we have enough neural cell, we can approximate any continuous function. Meanwhile, according the Kolmogorov–Arnold representation theorem, every multivariate continuous function. can be represented as a superposition of the two-argument addition of continuous functions of one variable, we can make many simple many to one neural cells for each variable to represent any continuous function. [Mybe I was wrong.]
Create and delete neural cell
Yes, In my DNA system, the neural cells will be dynamically created or deleted.
Neural cell creation
It’s a simulation of ‘fire together wire together’. When the passthrough(we consider it as the weight $w_A$) is large in neural cell A, we need to create a branch neural cell B to enhance this signal. Once we crate the neural cell B. A and B will equally share the passthrough
which means the initialization will be:
Neural cell deletion
On the opposite, we also need to delete the very less passthrough’s neural cell. We will just delete it and it’s input and output relation with other neural cells.
But how
Well, I still struggle in how to make a rule to tell us when we need to create the neural cells and when we need to delete the neural cells.
My naive idea for now is just create the new branch for top 10% high passthrough neural cells and delete the bottom 10% low passthrough neural cells. [TBD, need rethinking]
But When(Extinction)
In my plan, the neural creation and deletion process(sounds like model pruning) will be implement when we finish n epochs train and the loss not going down for more k epochs(refer the early stopping method, but we do not stop). And I name this process as a new term – ‘extinction’. It will be like, we have gone through many epochs in the history of our earth, and in some epochs we have met the species mass extinctions and entered another thriving epoch. Our DNA model, also, after n epochs, the model undergoes a mass extinction of neural cells, then the model enters to a new thriving epoch.
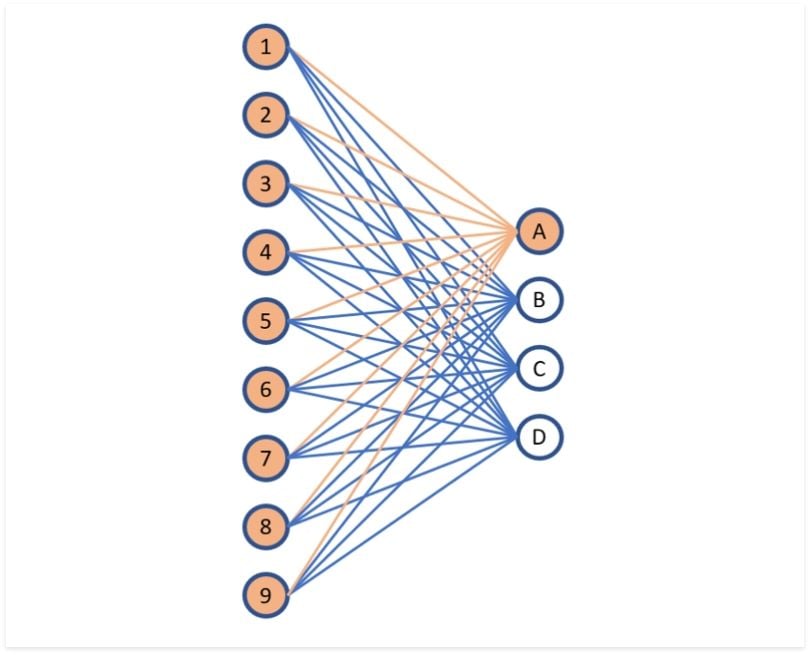
Model structure initialization
Before we train DNA model, we need to confirm the initial model structure. The initial model will just be like a Fully connected layer but each node in this layer is the single valuable(signal) and each edge in this layer is neural cell.
Beside, each neural cell’s trainable parameters $w$ and $b$ will be set to 1 and 0 respectively.
|  |
|
TODO
- Neural cell class
- Model data structure to manage each neural cell’s input and output
- Neural cell creation function
- Neural cell deletion function
- Extinction function
- Training example
- Result evaluation
Next level
- Forward-Forward algorithm or backpropagation-free method implement
- Neural cell distributing on different device(DAI).
- Self-perception, self-learning, and self-evolution.

